[문제] 백준 알고리즘 1932 (정수 삼각형)
> https://www.acmicpc.net/problem/1932
1932번: 정수 삼각형
문제 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5 위 그림은 크기가 5인 정수 삼각형의 한 모습이다. 맨 위층 7부터 시작해서 아래에 있는 수 중 하나를 선택하여 아래층으로 내려올 때, 이제까지 선택된 수의 합이 최대가 되는 경로를 구하는 프로그램을 작성하라. 아래층에 있는 수는 현재 층에서 선택된 수의 대각선 왼쪽 또는 대각선 오른쪽에 있는 것 중에서만 선택할 수 있다. 삼각형의 크기는 1 이상 500 이하이다. 삼각형을 이루고 있는 각 수는
www.acmicpc.net
부분 문제를 정의하여 점화식 찾기 + 누적하는 방식의 문제이다.
부분 문제를 위한 설명을 그림으로 그리면, 아래와 같다.
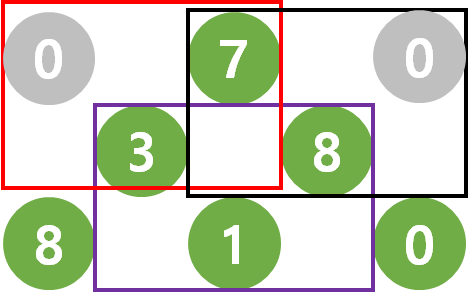
문제의 예제를 가지고 설명하면, 부분 문제는 간단하다. 빈 부분에 0이 있다고 가정하면 쉽다.
빨간색 박스를 기준으로 했을 때, 3 + (7 또는 0 중에 큰 것)이다.
입력 배열 tri[5][5]와 누적용 배열 dp[5][5]을 이용하여 점화식을 세울 수 있다.
|
idx |
0 |
1 |
2 |
|
0 |
7 |
||
|
1 |
3 |
8 |
|
|
2 |
8 |
1 |
0 |
유의할 점은 표와 같이, 7과 3의 idx가 같다는 점이다.
누적을 하면서 골라주기 위해서 큰 값을 고를 때, 누적 배열인 dp를 이용한다.
dp[0][0] = tri[0][0]
dp[1][0] = tri[1][0] + dp[0][0] (=tri[1][0] + max(0, dp[0][0]))
dp[1][1] = tri[1][1] + dp[0][0] (=tri[1][1]) + max(dp[0][0], 0))
dp[2][0] = tri[2][0] + max(0, dp[1][0])
dp[2][1] = tri[2][1] + max(dp[1][0], dp[1][1])
dp[2][2] = tri[2][2] + max(dp[1][1], 0)
...
이걸 점화식으로 나타내면, dp[i][j] = tri[i][j] + max(dp[i-1][j], dp[i-1][j-1])이 된다. (dp[0][-1] = 0 처리됨)
i>=1의 조건이므로 초기값 dp[0][0] = tri[0][0]과 배열 size > N이면 성립한다.
[문제 해결]
1. n과 tri[501][501] 배열에 입력
2. 초기값 dp[0][0] = tri[0][0]
3. 점화식 dp[i][j] = tri[i][j] + max(dp[i-1][j], dp[i-1][j-1]) 적용 (i=1~n-1, j=0~i)
4. dp[n-1]에서 최대값을 출력
[C++]
#include <cstdio>
#include <cstring>
using namespace std;
int n, tri[501][501], dp[501][501];
int max(int a, int b) {
if (a > b) return a;
else return b;
}
int main() {
memset(dp, 0, sizeof(dp));
memset(tri, 0, sizeof(tri));
scanf("%d", &n);
for (int i = 0; i < n; i++) {
for (int j = 0; j <= i; j++) {
scanf("%d", &tri[i][j]);
}
}
dp[0][0] = tri[0][0];
for (int i = 1; i < n; i++) {
for (int j = 0; j <= i; j++) {
dp[i][j] = tri[i][j] + max(dp[i-1][j], dp[i-1][j-1]);
}
}
int max_val = 0;
for (int i = 0; i < n; i++) {
max_val = max(max_val, dp[n-1][i]);
}
printf("%d", max_val);
return 0;
}
[Python]
import sys
input = sys.stdin.readline
n = int(input())
tri = [list(map(int, input().split())) for _ in range(n)]
dp = [[0] * n for _ in range(n)]
dp[0][0] = tri[0][0]
for i in range(1, n):
for j in range(i+1):
dp[i][j] = tri[i][j] + max(dp[i-1][j], dp[i-1][j-1])
print(max(dp[n-1]))
'백준 알고리즘(BOJ)' 카테고리의 다른 글
| 백준 알고리즘 2018 (통계학) - python (0) | 2021.07.24 |
|---|---|
| 백준 알고리즘 11653 (소인수분해) - python (0) | 2021.07.20 |
| 백준 알고리즘 2630 (색종이 만들기) - C++, Python (0) | 2019.11.08 |
| 백준 알고리즘 1149 (RGB거리) - C++, Python (0) | 2019.11.07 |
| 백준 알고리즘 9461 (파도반 수열) - C++, Python (0) | 2019.11.04 |
댓글