[문제] 백준 알고리즘 2751 (수 정렬하기 2) - C++, Python
> https://www.acmicpc.net/problem/2751
2751번: 수 정렬하기 2
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)이 주어진다. 둘째 줄부터 N개의 줄에는 숫자가 주어진다. 이 수는 절댓값이 1,000,000보다 작거나 같은 정수이다. 수는 중복되지 않는다.
www.acmicpc.net
수 정렬하기 1(2750)과 같은 문제이지만, 입력 N의 개수가 훨씬 많다.
> https://wlstyql.tistory.com/109
백준 알고리즘 2750(수 정렬하기) - C++, Python
[문제] 백준 알고리즘 2750(수 정렬하기) > https://www.acmicpc.net/problem/2750 2750번: 수 정렬하기 첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000)이 주어진다. 둘째 줄부터 N개의 줄에는 숫자가 주어진다. 이..
wlstyql.tistory.com
시간 복잡도 평균 O(NlogN)의 효율적인 정렬을 하는 문제이다.
병합 정렬, 힙 정렬, 퀵 정렬 등이 있는데, 힙 정렬을 구현해보기로 했다.
힙 정렬을 완전히 이해하는 데에 생각보다 시간이 오래 걸렸다.
힙 정렬은 최대 힙 트리나 최소 힙 트리를 이용한 정렬 방법이다.

위의 그림은 트리 기준이 아니라 배열 기준으로 설명 되어 있어서 헷갈린다.
자체적으로 예를 들어서, 이해하기 쉽도록 설명해보겠다.
아래 표와 같은 배열이 있다고 하자.

이 배열을 순서대로 이진 트리 구조로 만든다면, 아래의 그림처럼 된다.
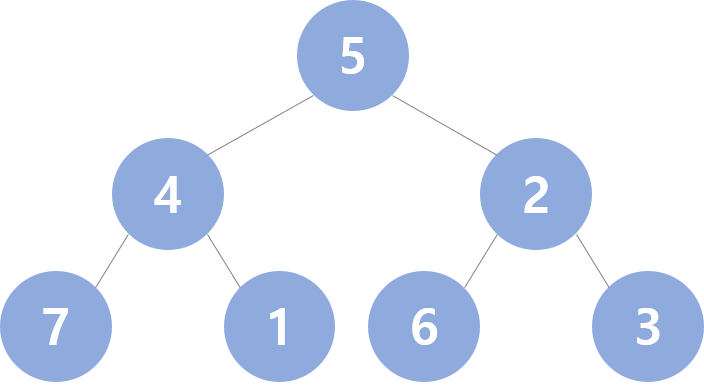
이 트리 구조는 최대 힙 구조를 만족하지 않는다.
최대 힙 구조는 부모 노드가 자식 노드보다 커야한다.
이제 최대 힙 구조에 맞게 힙 정렬을 해보기 위해, 아래와 같이 특정 영역을 지정했다.

이 영역을 배열에서 표시하면, 부모-자식 간에서 나타나는 특정 패턴을 알 수 있다.
[부모] [자식 - 왼쪽, 오른쪽]

위의 그림과, 다른 노드들을 이용하여 패턴을 식으로 만들면,
왼쪽 자식은 부모의 idx * 2 + 1, 오른쪽 자식은 부모의 idx * 2 + 2로 나타낼 수 있다.
부모와 자식의 val 값을 비교하여, 자식이 부모 val 값보다 크다면, 서로 값을 바꿔준다.
그렇게 되면, 아래와 같은 표와 노드가 된다.
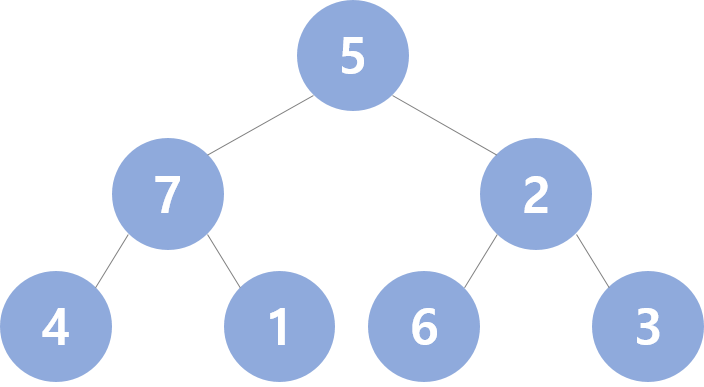

이 방식을 모든 부모-자식 간에 진행하면, 아래와 같이 최대 힙 트리 구조를 완성할 수 있다.
(부모를 기준으로 계산하면 되므로, (배열의 총 크기-1)//2번만 하면 된다.)


이제 최대 힙 트리 구조를 완성했으니, 힙 정렬을 해보자.
정렬은 최대 힙 트리에서 삭제(Delete) 방식을 이용한다.
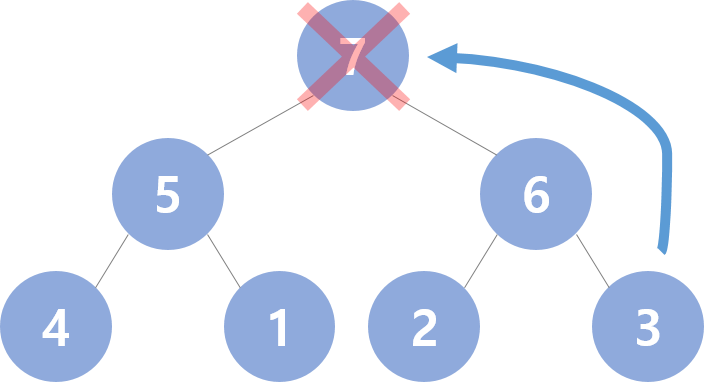
최대값(Root 노드)를 삭제하고, 마지막 노드를 대입하는 것이다.

이 상태에서, 다시 최대 힙 트리 구조를 만족하도록 다시 부모-자식 노드 값 비교를 진행한다.

다시 최대 힙 트리 구조를 만족하게 되었고, 최대 값이었던 7은 삭제되었다.
하지만, 우리는 정렬을 위해 최대값 7이 필요하므로, 빈 공간에 Fix 시켜놓도록하겠다.
그림으로 나타내면, 아래와 같이 나타낼 수 있겠다.

위와 같이 최대 힙 트리 삭제를 계속 진행하면, 힙 정렬이 완성된다.
(최대 힙 트리 구조에서, 루트와 마지막 노드를 바꾸고 진행하는 방식으로 구현하면 편리하다!)

[C++]
#include <cstdio>
#include <cstring>
using namespace std;
const int MAX = 1000000;
int n, heap[MAX];
void swap(int i1, int i2) {
int tmp = heap[i1];
heap[i1] = heap[i2];
heap[i2] = tmp;
return;
}
void max_heap(int cur, int size) {
while (cur < size) {
int left = cur * 2 + 1;
int right = cur * 2 + 2;
if (left < size || right < size) {
int tmp = cur;
if (left < size) {
if (heap[left] > heap[tmp]) tmp = left;
}
if (right < size) {
if (heap[right] > heap[tmp]) tmp = right;
}
if (tmp == cur) break;
swap(cur, tmp);
cur = tmp;
}
else break;
}
return;
}
void heapify() {
for (int i = (n - 1) / 2; i >= 0; i--) {
max_heap(i, n);
}
return;
}
int main() {
memset(heap, 0, sizeof(heap));
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d", &heap[i]);
}
heapify();
for (int i = n - 1; i > 0; i--) {
swap(0, i);
max_heap(0, i);
}
for (int i = 0; i < n; i++) {
printf("%d\n", heap[i]);
}
return 0;
}
[Python]
import sys
input = sys.stdin.readline
n = int(input())
L = [int(input()) for _ in range(n)]
def swap(i1, i2):
tmp = L[i1]
L[i1] = L[i2]
L[i2] = tmp
return
def max_heap(cur, size):
while cur < size:
left = cur * 2 + 1
right = cur * 2 + 2
if left < size or right < size:
tmp = cur
if left < size:
if L[tmp] < L[left]:
tmp = left
if right < size:
if L[tmp] < L[right]:
tmp = right
if tmp == cur:
break
swap(cur, tmp)
cur = tmp
else:
break
return
def heapify():
for i in range((n-1)//2, -1, -1):
max_heap(i, n)
return
heapify()
# max-heap delete-like sort
for i in range(n - 1, 0, -1):
swap(0, i)
max_heap(0, i)
for i in range(n):
print(L[i])
'백준 알고리즘(BOJ)' 카테고리의 다른 글
| 백준 알고리즘 1003 (피보나치 함수) - C++, Python (0) | 2019.10.27 |
|---|---|
| 백준 알고리즘 10989 (수 정렬하기 3) - C++, Python (0) | 2019.10.21 |
| 백준 알고리즘 2750 (수 정렬하기) - C++, Python (0) | 2019.10.16 |
| 백준 알고리즘 1956 (운동) - C++, Python (0) | 2019.10.16 |
| 백준 알고리즘 2206 (벽 부수고 이동하기) - C++, Python (0) | 2019.10.16 |

댓글